Розуміння, обчислення та вимірювання загальних гармонічних спотворень (THD)

Повне гармонійне спотворення (THD) - це вимірювання, яке повідомляє вам, яка частина спотворень напруги або струму обумовлена гармоніками в сигналі.

Повне гармонійне спотворення (THD) - це вимірювання, яке повідомляє вам, яка частина спотворень напруги або струму обумовлена гармоніками в сигналі. THD є важливим аспектом в аудіо, комунікаціях та енергосистемах і, як правило, але не завжди, повинен бути якомога меншим.

Гармонічні частоти періодичної напруги або струму

Гармоніки або гармонічні частоти періодичної напруги або струму є частотними складовими сигналу, які дорівнюють цілим кратним частотам основного сигналу. Це основний результат, який показує Фур'є-аналіз періодичного сигналу. Гармонічні спотворення - це спотворення сигналу внаслідок цих гармонік.

Напруга чи струм, які є суто синусоїдальними, не мають гармонічних спотворень, оскільки це сигнал, що складається з однієї частоти. Напруга або струм, які є періодичними, але не суто синусоїдальними, матимуть у собі високочастотні компоненти, що сприятимуть гармонічним спотворенням сигналу. Загалом, чим менше періодичний сигнал виглядає як синусоїда, тим сильнішими є гармонічні компоненти і тим більше гармонічних спотворень він матиме.

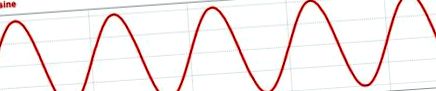
Отже, суто синусоїдальний сигнал не має спотворень, тоді як квадратна хвиля, яка є періодичною, але зовсім не виглядає синусоїдальною, матиме багато гармонічних спотворень. Звичайно, в реальному світі синусоїдальні напруги та струми не є абсолютно синусоїдальними; буде присутній деякий рівень гармонічних спотворень. На малюнках 1 і 2 наведено візуальне порівняння в часовій та частотній областях синусоїдальної напруги та прямокутної напруги.

Рисунок 1. Синусоїдальна напруга та напруга прямокутної хвилі у часовій області.

Рисунок 2. Синусоїдальна напруга та напруга прямокутної хвилі в частотній області; лише квадратна хвиля має піки на гармонічних частотах.

Легко побачити гармонійне спотворення при дослідженні подань часової області та частотної області квадратної хвилі, але також важливо мати можливість кількісно визначити гармонічні спотворення. У наступному розділі показано, як це зробити за допомогою метрики повне гармонійне спотворення.

Розрахунок загальних гармонічних спотворень

THD визначається як відношення еквівалентної середньоквадратичної (середньоквадратичної) напруги всіх частот гармонік (починаючи з 2-ї гармоніки) до середньоквадратичної напруги основної частоти (основна частота є основною частотою сигналу, тобто, частота, яку ви б визначили при дослідженні сигналу за допомогою осцилографа). Рівняння 1 показує математичне визначення THD (зауважте, що в цьому рівнянні використовується напруга, але замість нього може використовуватися струм):

$$ V _ $$ - середньоквадратична напруга n-ї гармоніки
$$ V _ $$ - середньоквадратична напруга основної частоти

Оскільки амплітуди гармонік необхідні для обчислення THD, для визначення THD може бути використаний аналіз Фур'є. Щоб побачити це застосування аналізу Фур’є, давайте розглянемо простий приклад квадратної хвилі 50% робочого циклу. Подання ряду Фур'є квадратної хвилі 50% робочого циклу є наступним:

І в розширеному вигляді це:

Розширену форму корисно переглянути, оскільки вона підкреслює пікову напругу (Vpk) кожної частотної складової, і THD можна розрахувати, визначивши середньоквадратичне значення (тобто $$ \ frac >> $$) кожної частотної складової та підключаючи їх усіх до рівняння 1:

Це рівняння починає ставати громіздким, але одне, на що слід звернути увагу, це те, що кожен член у виразі має компонент $$ \ frac \ pi> $$. Цей компонент можна розкласти на множники, і оскільки він з’являється як у чисельнику, так і в знаменнику, він фактично скасовується, що залишає вираз для THD квадратної хвилі наступним чином:

Для обчислення THD з цього виразу потрібна хитра математика. Якби підсумовування під квадратним коренем у рівнянні 5 починалося з n = 1, то це був би збіжний ряд, який дорівнює $$ \ frac $$:

Єдина різниця між виразом у рівнянні 6 та виразом THD рівняння 5 $$ \ left (\ sum _ ^ \ frac \ right) $$ - це значення $$ \ frac $$, коли n дорівнює 1. Оскільки це значення 1, підсумовування у виразі THD можна переписати як:

Нарешті, підключення цього рівняння назад до рівняння THD для квадратної хвилі (рівняння 5) дає:

Наше припущення на початку, що квадратна хвиля має багато гармонічних спотворень, базувалося на візуальному дослідженні квадратної хвилі в часі та частотній області. Розрахунки, які ми щойно пройшли, підтверджують наше припущення. Квадратна хвиля насправді має приблизно 48,3% загальних гармонічних спотворень, що означає, що середньоквадратичне значення гармонік становить приблизно 48,3% середньоквадратичного значення основної частоти.

Вимірювання загальних гармонічних спотворень

Обчислення теоретичного THD може бути гарною вправою, але це може бути великою роботою, і на практиці ви все одно не отримаєте ідеального сигналу (наприклад, ідеальної квадратної хвилі). Таким чином, результат цих розрахунків може дати лише приблизне значення THD, яке ви можете отримати для даного типу сигналу. На практиці THD потрібно виміряти, щоб отримати середньоквадратичне значення основної частоти та всіх гармонік. Це вимірювання можна зробити кількома способами.

У першому методі фільтри можна використовувати для розділення сигналу на дві частини: сигнал із усіма відфільтрованими гармоніками, що залишають лише основну частоту, і сигнал з відфільтрованою основною частотою, що залишає всі гармоніки. Тоді можна виміряти середньоквадратичне значення кожної з цих двох частин і розрахувати THD:

Перевагою цього методу є те, що ці вимірювання проводити легко. Недоліком є те, що шум також буде включений у вимірювання, тому ви насправді отримуєте вимірювання THD плюс шум (хоча в аудіосистемах THD + шум насправді теж є важливим виміром).

Другим методом вимірювання THD є вимірювання амплітуди основної частоти та кожної гармоніки, а потім використання цих вимірювань для обчислення THD за допомогою рівняння 1. Це вимірювання можна легко виконати за допомогою аналізатора спектра або аналізатора THD, який автоматично виконає рівняння 1 . Альтернативним методом вимірювання є захоплення даних напруги або струму, а потім виконання перетвореного Фур'є щодо зібраних даних. У наведеному нижче прикладі викладено, як використовується цей другий метод.

Приклад вимірювання THD

На прикладі блок-схеми на малюнку 3 показана синусоїда 1 кГц, що проходить через підсилювач, щоб створити нову синусоїду 1 кГц, яка має певні перехресні спотворення. Ця нова хвиля подається в аналізатор спектра, який дає графічне відображення амплітуди ряду гармонік.

Малюнок 3. Система, яка вводить перехресне спотворення в сигнал.

Наближаючи частотний спектр спотвореного виходу синусоїди, ми можемо побачити амплітуди на декількох гармонійних частотах:

Рисунок 4. Частотний спектр синусоїдальної напруги з перехресними спотвореннями.

З цього частотного спектру я вручну виміряв амплітуду кожної з гармонічних частот і записав дані в таблицю нижче:

Амплітуди гармонік спотвореної синусоїди

Гармонічний	Амплітуда
1	3,08В
3	0,308 В
5	0,159 В
7	0,090 В
9	0,0487 В
11	0,0253 В
13	0,0164 В
15	0,010 В

Амплітуди парних гармонік і гармонік вище 15-го складають майже 0, тому я не враховував їх у своєму розрахунку.

Виміряні амплітуди підключаються до рівняння THD:

(зауважте, що я можу використовувати амплітуди напруги замість середньоквадратичної напруги, оскільки $$ V_ = \ frac $$, а оскільки $$ \ sqrt $$ зустрічається в будь-який термін, його можна врахувати і скасувати).

Цей розрахунок дає THD 0,118 або 11,8%.

Звичайно, аналізатор THD може автоматизувати процес обчислення THD з амплітуд гармонік. Використання аналізатора THD для цього сигналу дає значення 11,9%, що підтверджує точність ручного методу, який я щойно пройшов.

Значення THD в системах

У цій статті наведено деякі відомості про THD та способи його визначення як теоретично, так і в реальній (змодельованій) системі. Але він не обговорював типи систем, де THD є важливим виміром.

THD важливий у кількох типах систем, включаючи енергосистеми, де низький THD означає вищий коефіцієнт потужності, менші пікові струми та вищу ефективність; аудіосистеми, де низький коефіцієнт THD означає, що звуковий сигнал є більш вірним відтворенням оригінального запису; та системи зв'язку, де низький коефіцієнт THD означає менші перешкоди для інших пристроїв і більшу потужність передачі для цікавить сигналу.

Шукайте майбутні статті, де я детальніше розкажу про ці конкретні типи систем.