Довгострокові тенденції старіння та довголіття людини

Анотація

За останні 200 років люди пережили величезне збільшення тривалості життя. Ці досягнення значною мірою були зумовлені зовнішніми поліпшеннями навколишнього середовища (наприклад, доступною дієтою, поширеністю хвороб, вакцинацією та станом гігієни та санітарії). У цій роботі ми запитуємо, чи буде подальше покращення тривалості життя обмежене згори тривалістю життя людини. Тривалість життя, на відміну від тривалості життя, осмислюється як біологічна міра довголіття, обумовлена внутрішньою швидкістю погіршення стану тіла. Для того, щоб продовжити своє питання, ми спочатку представляємо сучасну теорію старіння, розроблену біогеронтологами, і показуємо, що незмінна тривалість життя поставила б верхню межу тривалості життя. Потім для вибірки розвинених країн ми показуємо, що визначена таким чином тривалість життя людини була справді незмінною до середини ХХ століття, але з тих пір збільшувалась синхронно із тривалістю життя. Іншими словами, ми знаходимо докази виробленої тривалості життя.

Вступ

Для економістів тривалість життя людини є заданою константою. Це верхня межа Т що ми ставимо на знак інтегралу або суми, коли обчислюємо очікувану корисність ресурсу агента-репрезентанта. Тривалість життя концептуально відрізняється від тривалості життя. Хоча ми часто трактуємо тривалість життя, міру, яка залежить від ймовірності вижити від одного періоду до наступного, як константу, це припущення робиться "для зручності", оскільки виживання, безумовно, залежить від макроекономічного середовища (ВВП на населення, лікарі на квадратний кілометр тощо) та за окремими економічними рішеннями (харчування, витрати на охорону здоров'я тощо).

Хоча більша частина економічної теорії базується на спрощення припущення або про певне виживання до даного кінця життя, або про дану не пов'язану з віком ймовірність виживання в одиниці часу життя (на основі Yaari 1965 та Blanchard 1985), існує також Зараз багата література, яка намагається ендогенізувати виживання та включити емпірично вірогідні ймовірності виживання в економічні міркування. Однак, наскільки нам відомо, в економічній науці не існує досліджень тривалості життя людини. Виноска 1

На відміну від тривалості життя, яка залежить від населення та ситуації, тривалість життя, як правило, осмислюється як видоспецифічні характеристика (Arking 2006; Гаврилов та Гаврилова 1991). Наприклад, тривалість життя популяції мишей, наприклад, залежить від конкретного середовища в дикій природі або в лабораторії. Тривалість життя мишей, навпаки, не залежить від таких умов, але вона відрізняється від тривалості життя плодових мух або слонів. Так само тривалість життя певної людської популяції різниться в різних країнах (Англія проти Уганди) і з часом (Англія сьогодні проти 200 років тому). Однак тривалість життя людей, якщо вона існує, повинна бути незмінною серед різних груп населення. Напевно, всі біологи погоджуються з цим поняттям тривалості життя. Але як виміряти тривалість життя - на відміну від тривалості життя - домовитись менш легко.

Визначення тривалості життя людини як максимально досяжного віку смерті, як пропонується у багатьох загальних словниках та багатьох старих внесках у біологію, безумовно, вводить в оману (Wilmoth 1999; Carey 2003). Концептуально цю ідею спростовує розуміння того, що "скільки б нам не було років, наша ймовірність померти протягом наступної години ніколи не дорівнює одиниці" (Jacquard 1982). Емпірично, це спростовується спостереженням, що максимальний вік смерті постійно зростав щонайменше 140 років (Wilmoth and Robine 2003).

Простий факт, що «обсяг вибірки» людей, які коли-небудь жили на землі, постійно зростає, дозволяє нам сподіватися, що максимальна тривалість життя, що спостерігається, зростатиме з плином часу. Це вражаюче показали Фінч і Пайк (1996). Вони визначають тривалість життя Т як передбачуваний вік смерті останнього вижившого з популяції такий, що \ (S (x) = 1/N \) - це ймовірність бути останнім чоловіком, що виділяється з N. Підключення 1 /N в емпірично оцінену функцію виживання Гомперця вони отримують тривалість життя 105 років для \ (N = 10 ^ 3 \) і 114 років для \ (N = 10 ^ 7 \). Взагалі, залежність максимумів від обсягу вибірки є загальновідомим фактом статистики екстремальних значень (Gumbel 1958).

З цих спостережень повинно бути зрозуміло, що тривалість життя, на відміну від тривалості життя, не може бути визначена як просто статистичний показник без біологічного обґрунтування. Нам потрібно трохи зрозуміти біологічний механізм старіння, щоб зробити висновок про внутрішній механізм, який регулює темпи погіршення нашого тіла. Дотримуючись стандартних міркувань у сучасній біології, приймаючи старіння та смерть як стохастичні процеси (Arking 2006), ми цікавимось, чи існує закономірність, яка є спільною для всіх людей незалежно від екологічних та генетичних характеристик. З цієї закономірності, якщо вона існує, ми намагаємось зробити висновок про тривалість життя не як абсолютний максимум, а як характерну тривалість життя. Виноска 2

Ми починаємо своє прагнення до тривалості життя людини у Розділі 2, вводячи дві дуже сильні емпіричні закономірності - закон смертності Гомперца – Макегема та компенсаційний ефект смертності. Ці емпіричні закономірності теоретично підтверджуються теорією надійності, як це показали Гаврилов, Гаврилова (1991) та інші біогеронтологи. Це призвело до розробки нової теоретично обґрунтованої концептуалізації тривалості життя людини. Суть цієї теорії та її наслідки ми накреслимо в розділі 2.3. Найважливішим кількісним наслідком є те, що тривалість життя людини можна зробити з оціночного компенсаційного ефекту смертності. У розділі 3 ми показуємо, що тривалість життя людини, якби вона була незмінною, призвела б до прямокутника кривої виживання і, таким чином, поставила б верхню межу на майбутні досягнення людського довголіття.

У розділі 4 ми оцінюємо параметри рівняння Гомперца – Макегема, використовуючи метод нелінійних найменших квадратів та дані про вікові показники смертності з бази даних смертності людей (2010). Потім ми використовуємо оцінені параметри для аналізу компенсаційного ефекту смертності та висновку про тривалість життя людини. Ми спостерігаємо інваріантний до часу компенсаційний ефект до середини ХХ століття для всіх країн нашої вибірки. У другій половині ХХ століття ми знаходимо докази світського збільшення тривалості життя людини. Іншими словами, ми виявляємо, що людська винахідливість ефективно втручалася в природу і створила "виготовлене життя" (Carnes and Olshansky 2007). Нарешті, ми показуємо, що тривалість життя у другій половині минулого століття зростала синхронно із тривалістю життя. Значною мірою і все більше ми живемо довше, оскільки технічний прогрес змінив спосіб старіння та спосіб розпаду нашого тіла.

Наше дослідження продовжує роботу Штрелера та Мілдвана (1960) та Гаврилова та Гаврилової (1991). Порівняно з цими попередніми роботами, ми використали більшу вибірку, що складається з більшої кількості країн і охоплює значно довший проміжок часу. Це дозволило нам не тільки підтвердити більш ранній результат інваріантного в часі компенсаційного ефекту (інваріантний тривалість життя) до середини ХХ століття, а й на основі нових даних кінця ХХ століття отримати новий результат світське збільшення тривалості життя людини. Цей висновок, у свою чергу, дозволив нам запропонувати нове пояснення спостереження за “порушеними межами тривалості життя” (Oeppen and Vaupel 2002): приблизно з 1970-х років пізніше народжені люди можуть розраховувати жити довше, принаймні частково, тому що тривалість життя людини зростає.

Тривалість життя людини: теорія

Закон смертності Гомперца – Макехема

Усі теорії тривалості життя людини базуються на дуже сильній емпіричній закономірності - законі смертності Гомперца – Макегема. Він бере свій початок від актуарія Бенджаміна Гомперца (1825), який зауважив, що існує тривалий період життя, коливається приблизно від 30 до 90 років, для якого вік та смертність лінійно лінійно пов'язані. Нехай \ (\ mu (x) \) позначає символ сила смертності, тобто умовна ймовірність смерті у віці х з даним виживанням до віку х. Тоді закон Гомперца офіційно формулюється як \ (\ mu (x) = R \ exp (\ alpha x) \). Зазначивши, що не всі причини смерті пов'язані з віком, Макехем (1860) додав константу \ (A \ ge 0 \), яка забезпечує відому формулу Гомперца – Макема:

Враховуючи як простоту, так і точність, формула Гомперца – Макема на сьогоднішній день є найбільш підходящим, стислим та широко використовуваним офіційним описом старіння (Ольшанський та Карнес 1997). Його параметри оцінюються з великою точністю з \ (R ^ 2 \) вище 0,9 не тільки для людей, але і для таких різних видів, як дріжджі, плодові мухи та коні. Оцінені коефіцієнти, звичайно, сильно відрізняються, що відображає великі коливання у тривалості життя у різних видів (Arking 2006).

Використовуючи закон Гомперца – Макема і вирішивши \ (\ точка S (x)/S (x) = - \ mu (x) \), ми отримуємо безумовну ймовірність вижити до віку х. Враховуючи, що \ (S (0) = 1 \), ми приходимо до рівняння 2:

Від S(х), ми можемо зробити висновок про тривалість життя (очікувані залишкові роки життя) у віці х як \ (L (x) = ^ S (a) \ mathrm a/S (x)> \) .

За останнє століття тривалість життя людини при народженні зросла більш ніж на 20 років у більшості повністю розвинених країн (Riley 2001). Цікаво дослідити, як ці величезні вдосконалення людського довголіття фіксуються законом Гомперца – Макехема. Для цього корисно виділити параметр Makeham A оскільки він відображає не пов'язані з віком сили смертності, тобто фонову смертність (Bongaarts 2005) або зовнішню смертність (Carnes and Olshansky 2007). Ми очікуємо, що запобігання, викорінення або лікування вікових захворювань відобразиться на змінах A. Навпаки, будь-який прогрес щодо самого процесу старіння відображався б у зміні вікових параметрів Гомперца Р. і α. Як видно з рівнянь. 1 і 2, нижній Р. означало б, що люди починають із покращеним здоров’ям (у молодості) та нижчим α означало б, що швидкість процесу старіння сповільнюється. Однак, як показано в розділі 2.3, ми очікуємо цього α і Р. не змінюються самостійно, доки тривалість життя людини є незмінною.

За останні два століття фонова смертність різко знизилася в сучасних повністю розвинених країнах (наприклад, для Швеції з \ (5,5 \ cdot 10 ^ \) до \ (4,8 \ cdot 10 ^ \); Гаврилов та Гаврилова 1991). С A будучи близьким до нуля, майбутній прогрес у тривалості життя повинен відбуватися завдяки покращенню вікової залежності смертності. Іншими словами, якби технічний прогрес міг вплинути лише на смертність, але не на внутрішню швидкість розпаду тіла, спостерігається тенденція до збільшення тривалості життя при народженні приблизно на 3 місяці на рік народження (Oeppen and Vaupel 2002) майбутнє. Натхненні цим фактом, деякі геронтологи дійшли висновку, що тривалість життя в майбутньому при народженні навряд чи перевищить 85 років (Fries 1980; Carnes and Olshansky 2007). Проблема такої гіпотези полягає в тому, що - хоча практично нульова смертність не залишає можливостей для поліпшення - ми не можемо (поки) бачити будь-яке уповільнення або зближення тривалості життя в даних (Wilmoth 1997, 1999). Це означає, що останні досягнення середньої тривалості життя, мабуть, відбулися в процесі, який відображається зміною параметрів Гомперца.

Компенсаційний ефект смертності

Параметри Гомперца α і Р., які оцінюються з високою точністю для дано населення різняться фактично за статтю, за країнами та з часом. Це означає, що, хоча всі люди, здається, старіють відповідно до загального загального закону смертності, конкретні параметри, що регулюють цей закон, залежать від статі, походження та часу. Крім того, Р. і α здається, залежить також від географії та має тенденцію до падіння (у випадку з Р.) або піднятися (у випадку α) з економічним розвитком. Через свою нестабільність параметри Гомперца як такі не підходять для визначення тривалості життя людини.

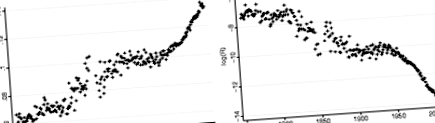
Однак параметри Гомперца не змінюються незалежно один від одного, але, що вражає, певним чином, таким чином, що вони зберігають зворотну зв'язок між α і журнал Р.. Цей факт відомий як кореляція Штрелера – Мілдвана або компенсаційний ефект смертності (Strehler and Mildvan 1960; Gavrilov and Gavrilova 1991). Це наочно показано для Швеції на рис. 1 і 2. На рисунку 1 показані довгострокові тенденції розвитку α і Р.. З часом параметр нахилу α має тенденцію до зростання і параметр рівня Р. має тенденцію до падіння. Це означає, що з часом шведські жінки, як правило, старіють швидше, але починають із нижчої початкової смертності. Нижче ми показуємо загальність цього явища по країнах і те, як це можна пояснити збільшенням початкової надмірності в теорії надійності старіння.

Тенденції старіння шведських жінок у 1751–2005 рр. Ліва панель: Розробка α через деякий час. Права панель: Розробка Р. через деякий час